Pěšcové koncovky – trénink GM Marek Vokáč s domácím úkolem

Koncovka je fáze partie, ve které se na šachovnici vyskytuje už jen malé množství materiálu. Některé partie pravda do fáze koncovky nedojdou, pokud se jednomu z hráčů podaří dát soupeři mat dříve. To ale vůbec není tak snadné, mnohem častěji v průběhu partie jedna ze stran postupně získává malinké výhody, které se teprve ve fázi koncovky podaří proměnit ve vítězství. Zřetelnou a srozumitelnou výhodou je například materiální převaha. Podaří se vám třeba během partie soupeřovi sebrat o jednoho pěšce více, než dokázal on. Máte tak převahu jednoho pěšce. To je ale ta nejmenší možná materiální převaha, která se při plné šachovnici figur vůbec nemusí projevit.

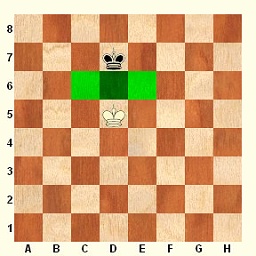
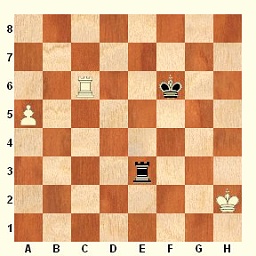
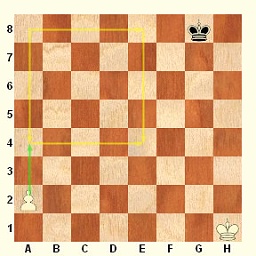
Například ve fotbale se občas stane, že je někdo ze hry vyloučen, a na hřišti pak bojuje 11 fotbalistů proti 10 fotbalistům. To je samozřejmě velká výhoda, přesto se však často vůbec neprojeví počtem vstřelených branek, a někdy dokonce v zápase vyhraje strana, která většinu času měla o jednoho hráče méně. Když si ale půjdete zahrát fotbal někam do parku, a budete hrát 2 proti jednomu, šance onoho osamělého bojovníka na úspěch je velice malá, to by musel být opravdu vynikající hráč. Rozdíl v počtu hráčů je sice stejný, ale poměr 11:10 je trochu jiný než poměr 2:1. Čím méně hráčů na hřišti je, tím výraznější dopad má rozdíl v jejich počtu.

V šachu platí něco podobného. Velmi zjednodušeně v koncovce král a pěšec proti králi je jisté, že osamocený král již partii vyhrát nemůže. Vlastník pěšce však tuto šanci stále má. Jedním pěšcem sice mat dát nejde, ale jistě si pamatujete, že pokud pěšec projde až na 8. řadu, může být proměněn například v dámu, nu a matit králem a dámou samotného krále již umíte. To je velmi jednoduchý způsob, jak v koncovce využít převahu toho jednoho zdánlivě slaboučkého a bezvýznamného pěšce!

Pěšcové koncovky jsou nejjednodušší koncovky, které vám mohu nabídnout. Tím rozhodně nechci tvrdit, že jsou nejsnadnější pro hru. Jsou ale nejsnadnější pro pochopení. Vystupují v nich totiž jen králové a pěšci. Ti se vyskytují prakticky ve všech typech koncovek, proto se nejdříve naučíme, jak spolu navzájem spolupracují sami. Ono to totiž bude většinou platit i v případech, kde se do hry v koncovce budou zapojovat i další figury. Formy spolupráce dvou různých typů figur jsou totiž pořád stejné, to přítomnost jiných figur na šachovnici ovlivnit nemůže. Může však významně bránit v použití těchto forem spolupráce.

9.2.1 Nauka o čtvercích

Základem pěšcových koncovek je boj krále a 1 pěšce proti králi. Zde nejde o to dát soupeřovu králi mat. Cílem této koncovky je průnik pěšce na 8. řadu (nebo na 1. řadu, pokud je černý) a jeho proměna v dámu. Vytvořením nové dámy se pěšcová koncovka mění ve známé matové vedení králem a dámou. Úkol je jasný, jak ho ale splnit? Někdy to dokáže pěšec sám!

Diagram 1 ukazuje velmi snadný příklad. Úkolem bílého pěšce je dojít z pole b5 na pole b8. Bílý pěšec stojí na sloupci b, pole b8 se nazývá „pole proměny pěšce b“. Musí tedy provést tahy 1. b6, 2. b7, a 3.b8D. Pouhé 3 tahy, a pěšec se mění v dámu, převaha bílého je náhle obrovská a zbývá už jen dát černému králi známý mat. Může proti tomu černý něco podniknout? Má pouze krále, může tedy hrát pouze králem. Jeho jedinou nadějí je bílého pěšce na cestě k poli proměny zastavit, nejlépe svým králem tohoto pěšce sebrat. Dokáže to černý král? Jak to zjistíme?

Můžeme si to prostě spočítat. Metoda „Já sem, ty tam, já pak tam, ty pak tam atd.“ je to nejjednodušší, co může šachista vymyslet. Představí si prostě další průběh partie. Pokud je bílý na tahu, může zahrát 1.b6. Černý král musí pěšce pronásledovat, směřovat rovněž k poli jeho proměny, zde k poli b8. Například tedy 1…Kd4. A partie pokračuje 2.b7 Kc5 3.b8D. Velmi rychle je jasné, že pěšec černému králi utekl, a vzniku nové dámy černý zabránit nemůže. Zachránilo by ho již pouze to, kdyby nyní právě zrozenou dámu mohl králem sebrat. Jenže to se zde nedá, pole b8 je od pole c5 příliš daleko. Druhá metoda vypadá vědecky: „Kolik tahů já, kolik tahů on“ Spočítáme počet tahů, které musí bílý udělat pěšcem k poli proměny – jsou přesně 3, po tom posledním se zrodí nová dáma. To se dá snadno vyčíst ze šachovnice, pole b5 je od pole b8 vzdáleno 3 pole (3 řady), pěšec potřebuje 3 tahy. Černý král na poli e3 je od pole b8 vzdálen 5 řad a 3 sloupce. Král se sice může pohybovat i po diagonálách, ale to není pro výpočet rozhodující. Počet nezbytných tahů určuje vyšší číslo z těchto dvou čísel, v tomto případě je to tedy nejméně 5 tahů. Král může jít k poli b8 několika cestami, ale nejkratší bude trvat nejméně 5 tahů. 5 tahů je více než 3 tahy, pěšec je tedy o 2 tahy rychlejší, a král ho zastavit nedokáže. Obě naznačené metody jsou použitelné, ale pro začátečníka poněkud nejisté – vyžadují trochu cviku a představivosti, navíc musí věnovat pozornost tomu, kde přesně král a pěšec stojí, každý jiný příklad musí zkoumat jako nový problém, vše pěkně od začátku. Jako ukázka nám poslouží i pouhá změna začínajícího hráče. Jak tato koncovka dopadne, pokud bude první na tahu černý?

První metoda odhalí tento průběh boje: 1…Kd4 2.b6 Kc5 3.b7 Kb6 4.b8D+. Černý král opět přišel pozdě, bílý pěšec se proměnil v dámu a následuje matové vedení. Druhá metoda zjistí, že svým úvodním tahem může černý počet svých tahů k poli b8 snížit z 5 na 4, to je ale stále více než 3 tahy pěšce, a pěšec by tedy měl v závodě zvítězit. Toto je velmi jednoduchý příklad, postup obou metod je proto jednoduchý a mohlo by se zdát, že je jedno, jakou metodu hráč zvolí. Přijdou ale i složitější situace, a tam už výpočet nemusí být tak snadný.

Šachisté mají rádi zásady a poučky, které platí ve stejném znění pro různé obecné případy. A pro náš případ už hodně dávno někdo vymyslel velmi prostou poučku. Všiml si totiž, že každého pěšce utíkajícího k poli proměny je možno charakterizovat jednoznačným čtvercem polí. Tento čtverec je znázorněn na diagramu 2. Pěšec stojí na poli b4. Čtverec tohoto pěšce určíme tak, že z pole b4 vyrazíme v myšlenkách na 8. řadu po diagonále, která polem b4 prochází. Zde jde o část diagonály a3-f8, kterou tvoří políčka mezi b4 a f8 (pole b4, c5, d6, e7 a f8). Tato políčka představují úhlopříčku našeho pomyslného čtverce (vyznačeno zelenou šipkou). Jeden vrchol čtverce tvoří pole b4, na kterém pěšec stojí. Druhý vrchol čtverce tvoří pole f8, tedy pole na úhlopříčce b4-f8 a na 8. řadě (matematik by řekl průnik). Zbývá už jen konstrukci čtverce dokončit. Dalším vrcholem čtverce je pole proměny pěšce, tedy pole b8, a poslední vrchol vytváří průnik 4. řady (na ní stojí pěšec) a sloupce f (na něm je diagonální pole f8). Tak jsme vytvořili čtverec pěšce b4, jeho vrcholy tvoří pole b4, b8, f8 a f4. A proč se tak namáháme s vytvářením jakéhosi čtverce? Protože z něho vyplynula následující poučka:

1. Pokud král může svým tahem vstoupit do čtverce soupeřova pěšce, pak dokáže pěšce v cestě na pole proměny zadržet.

Na diagramu 2 je jasně vidět, že pokud je černý na tahu, může jeho král provést tahy 1…Ke4, nebo 1…Kf4, oběma tahy vstoupí do čtverce pěšce b4 a stihne pěšce sebrat nejpozději ve chvíli, kdy se pěšec na poli b8 proměňuje v dámu – například 1…Kf4 2.b5 Ke5 3.b6 Kd6 4.b7 Kc7 5.b8D+ Kxb8. Povšimněte si rovněž, že pokud by černý král šel na jiné pole, např. 1…Kg4 nebo 1…Ke3, pak by těmito tahy do čtverce pěšce b4 nevstoupil, a pěšec by mu utekl!

A co by se stalo, kdyby byl na diagramu 2 na tahu bílý? Zahrál by jednoduše tah 1.b5, a čtverec bílého pěšce by se zmenšil! Tvořily by ho totiž vrcholy b5, b8, e8 a e5 – čtverec pěšce se mění po každém tahu, který pěšec provede! A to by zde byla pro černého krále nepříjemná zpráva, protože z pole f3 by se do nově vytvořeného čtverce již nedokázal svým následujícím tahem dostat! Zůstal by v každém případě mimo čtverec pěšce, a pěšec by se bez problémů na poli b8 proměnil v dámu.

Nu ovšem, už vidím, jak se někdo nadechuje k otázce. Proč mluvíme o jednom čtverci, když polem b4 procházejí diagonály dvě, a mohli bychom tedy zkonstruovat čtverce dva? Podíváme se na další diagram 3. Každým polem šachovnice procházejí 2 diagonály, teoreticky tedy můžeme vždy konstruovat 2 čtverce, i když to okraje šachovnice budou deformovat. Například pěšec na poli d5 opravdu umí vytvořit 2 čtverce, jeden je vyznačen zeleně, druhý žlutě. Pravidlo čtverce je možno použít na oba dva čtverce, prakticky má ale význam jen jeden z nich. Pravidlo čtverce totiž nevyjadřuje jen vlastnost pěšce, ono vyjadřuje spíše vztah mezi utíkajícím pěšcem a bránícím králem. A proto má smysl zabývat se pouze čtvercem, který je vytvořen v oblasti mezi pěšcem a králem. Na opačné straně pěšce se totiž v jejich souboji nic zvláštního zatím odehrávat nebude.

Diagram 4 je vážným varováním pro zapomnětlivé! Pěšec v základním postavení má právo udělat dvojkrok, přemístit se tedy okamžitě o 2 pole vpřed. To král v žádném případě nedokáže, proto je třeba mít na paměti, že čtverec pěšce v základním postavení je nutno konstruovat jinak než ostatní čtverce. Pěšec a2 na diagramu 4 vytváří čtverec s vrcholy na polích a3, a8, f8 a f3! Pokud vytvoříte čtverec z polí a2, a8, g8, a g2, pak pěšec svým následujícím tahem 1.a4 může tento čtverec zmenšit ihned o 2 pole v každém směru. Pokud je v pozici diagramu 4 na tahu černý, pak musí vstoupit do čtverce pěšce a3, aby po očekávaném dvojkroku pěšce a2 ještě stihl vstoupit do čtverce pěšce a4, musí tedy zahrát 1…Kf8 nebo 1…Kf7, a po 2.a4 hrát např. 2…Ke8 a pěšec mu neunikne.

Cvičení:

1. Vyznačte čtverce bílých pěšců stojících na poli: a5; d3; h4, e7; c2; g5; f6; b2.

2. Vyznačte čtverce černých pěšců stojících na poli: d7; b3; e5; f2; a6; g7; h4; a5

Přestávka

9.2.2 Opozice

Kapitola o čtvercích se věnovala souboji osamoceného pěšce s bránícím králem. Druhý král na šachovnici jen přihlížel. V drtivé většině pěšcových koncovek tomu tak ovšem není. I když jde o pěšcové koncovky, jejich jádrem je obvykle souboj králů. Král je totiž určitě silnější figura než pěšec, má bohatší arzenál tahů a nejen v pěšcových koncovkách hraje výraznou, ne-li přímo rozhodující roli. Král si musí počínat v koncovce aktivně, vzhledem k omezenému materiálu je již významnou bojovou jednotkou, navíc se nemusí tolik bát matových hrozeb. Boj králů je především bojem o prostor, o průnik na důležitá pole šachovnice. Boj králů je především bojem o opozici. To je slovo, které záhy straší studenta pěšcových koncovek i ve snu. Opozice je v šachu vyjádřením určité rovnováhy. Zase si to ukážeme na příkladu.

Diagram 5 ukazuje základní typ jednoduché opozice králů. Králové na d5 a d7 stojí v opozici, zónu rovnováhy mezi nimi představují vyznačená pole c6, d6 a e6. Ani jeden z obou králů nyní nemůže postoupit vpřed (do zóny rovnováhy), soupeřův král kontroluje všechna důležitá pole. Hráč, který je v této pozici na tahu, je v nevýhodě! Musí svým králem provést tah, přitom každým svým tahem rovnováhu poruší, aniž by dosáhl nějaké výhody. Naopak, jeho soupeř po libovolném tahu získá nějakou možnost vstoupit do zóny rovnováhy. Podobným situacím se říká nevýhoda tahu. To je nebývalá věc! Málo her umí pracovat s tím, že provedení tahu může hráče poškodit, zhoršit jeho šance. V šachu, a zvláště v koncovkách, je nevýhoda tahu velmi důležitý prostředek hry, který se používá velice často. Důležité je, kdo je útočník, a kdo je obránce. To se nelosuje házením mincí nebo hlasováním poroty. O tom rozhoduje celkové postavení na šachovnici. Útočníkem rozumíme toho hráče, který by vniknutím na pole rovnováhy získal významnou výhodu. Není nijak neobvyklé, že útočníkem a obráncem najednou jsou obě strany. Pokud je například na diagramu 1 úkolem proniknout králem na 8. řadu (bílý) nebo 4. řadu (černý) dříve než to dokáže soupeř. Útočníkem pak jsou oba králové, a hráč, který je v pozici na tahu, tento souboj prohraje. Pokud je například na tahu bílý, pak je celkem jedno, jestli zahraje 1.Ke5 nebo 1. Kc5. Černý král poté vstoupí na uvolněné pole rovnovážné zóny, tedy například 1.Ke5 Kc6. Černý král je rázem blíže ke 4. řadě než bílý k 8. řadě. Bílý se může pokusit bránit tahem 2. Kd4, načež černý použije manévr pro boj v opozici zcela typický – vytvoří novou opozici tahem 2…Kd6!, a bílý se znovu ocitne v nevýhodě tahu a musí znovu černému králi uvolnit cestu. Máte pravdu, černý by mohl pokračovat i přímo ke 4. řadě tahem 2…Kb5 a splnit úkol následujícím tahem 3…Ka4. Zadání úkolu totiž bylo příliš široké, 4. řada je jako cíl příliš velká. Pokud by bylo úkolem proniknout na jedno z polí c4+d4+e4, pak by černý musel manévrovat opakovanou opozicí.

Když jste se učili hrát králem v 1. lekci, hráli jste cvičnou hru královský fotbal. Ta hra je jednoduchým cvičením opozice, ačkoliv králové začínali z polí e1 a e8. Diagram 6 vám napoví, proč velká vzdálenost mezi králi může být stejně cvičením opozice. Opozice totiž v postavení nemizí! Zóna rovnováhy někde na šachovnici neustále existuje, je to oblast mezi výchozí polohou obou králů, ke které se oba mohou dostat stejným počtem tahů. Na diagramu 6 stojí králové na polích e3 a e7, zónou jejich rovnováhy je 5. řada stejně, jako kdyby králové stáli třeba na polích e4 a e6. Nabídnu jednoduchou pomůcku pro rozeznání opozice a zóny rovnováhy. Na obou diagramech je možno objevit společný znak. Oba králové stojí na stejném sloupci, na poli stejné barvy, a počet polí mezi nimi je lichý (1, 3). Postavení na diagramu 6 se nazývá vzdálená opozice. Pokud se hráč na tahu rozhodne k soupeřovu králi přiblížit, pak na každý jeho tah může soupeřův král zaujmout novou opozici s vlastnostmi diagramu 5: 1.Ke4 Ke6, nebo 1.Kd4 Kd6, nebo 1.Kf4 Kf6. Záludnější okamžik nastane ve chvíli, kdy se bílý rozhodne králem nepřibližovat, a zvolí vyčkávací tah, například 1.Kd3. Černý pak může reagovat tahem 1…Kd7, tím si udržuje vzdálenou opozici, ale nepostoupil vpřed. Po dalším 2.Ke3 Ke7 by mohli králové tato pole řádně podupat, aniž by v pozici došlo k nějakému pokroku. Tak se ovšem nevýhoda tahu využít nedá. Černý musí opozici využít aktivnějším postupem 1…Kf6!, podobně jako v případě diagramu 5. Černý král postoupil vpřed na takové pole, proti kterému bílý král nemůže zaujmout postavení opozice. Chybou by naproti tomu bylo 1…Ke6? pro 2.Ke4, nebo 1…Kd6? pro 2.Kd4, v těchto případech svým tahem bílý do opozice vstoupí, a role králů se vymění, v nevýhodě tahu by se ocitl černý král. Po tazích 1.Kd3 Kf6! nic takového bílý nedokáže, má na výběr buď vstoupit králem zpět na sloupec e, pak černý na tomto sloupci opozici obnoví (tedy 2.Ke3 Ke5!, nebo 2.Ke4 Ke6!) a boj pokračuje metodou ukázanou na diagramu 5. Nejrafinovanější je z pohledu bílého tah 2.Ke2!?, na který má černý jen jednu správnou odpověď – tah 2…Ke6! znovu vytvoří situaci vzdálené opozice, jen se celé postavení posunulo o řadu níže do tábora bílého. Pokud se bílý král na sloupec e nevrátí, černý král bude pokračovat v postupu vpřed po sloupci f, stejně, jako se choval na diagramu 5.

Aby vás to nespletlo, když si postavíte krále do výchozího postavení na pole e2 a e8, nebo e1 a e7, pak před vámi znovu stojí případ opozice, je ještě vzdálenější než na diagramu 6, ale platí pro ni stejné zásady a stejné postupy jako na diagramech 5 a 6. A opozice je samozřejmě i situace, kdy králové stojí na polích c4 a e4, pak je ovšem zónou jejich rovnováhy sloupec d, boj o rovnováhu probíhá v jiné oblasti, ale zásady jsou stále stejné.

Cvičení:

Toto cvičení bude trochu netradiční. Už jsme na téma opozice hráli v lekci 1 královský fotbal, nyní přidáme druhou tematickou hru. Cvičení 1 z výchozí pozice diagramu 7 má neobvyklé zadání: Bílý na tahu vynutí mat černému králi tak, že svou věží provede během matového vedení jen jeden jediný závěrečný matový tah, všechny ostatní manévry musí provést svým králem!

Cvičení 2 nabízí z pozice diagramu 8 již plnohodnotný boj obou králů. Začínat může bílý nebo černý, to podle vašeho vkusu. Hraje se regulérní partie, tedy až do matu. Hlavním úkolem je ale pokus o stanovení objektivního výsledku hry z pozice diagramu 8, pokud obě strany hrají nejlepší tahy. Nemám to srdce nechat správné řešení obou cvičení na vyučujícím, ale schovám si ho až do kontroly domácích úkolů v následující lekci.

Domácí úkol:

Domácí úkol už bude vyžadovat trochu více práce. Úlohy 32 a 33 vyžadují správně spočítat závody krále a pěšce, jen pěšců je trochu více, a u digramu 33 je trochu potřeba i myslet.

Úloha 34 je typický příklad ze života. Jestli může černý měnit věže, o tom rozhoduje pouze správný propočet vznikající pěšcové koncovky. Ten je zde samozřejmě ještě velmi snadný. Mnohem těžší je poslední úloha 35. Bílý totiž musí vymyslet něco, o čem jsme zatím nijak významně nehovořili. Ale ten, kdo pozorně poslouchal lekci o tom, jak se po šachovnici pohybuje král, by na to přijít měl.